数学建模专栏 | 第三篇:MATLAB数据建模方法(上) —常用方法
作 者 简 介
卓金武,MathWorks中国高级工程师,教育业务经理,在数据分析、数据挖掘、机器学习、数学建模、量化投资和优化等科学计算方面有多年工作经验,现主要负责MATLAB校园版业务。曾2次获全国大学生数学建模竞赛一等奖,1次获全国研究生数学建模竞赛一等奖。
以数据为基础而建立数学模型的方法称为数据建模方法, 包括回归、统计、机器学习、深度学习、灰色预测、主成分分析、神经网络、时间序列分析等方法, 其中最常用的方法还是回归方法。 本讲主要介绍在数学建模中常用几种回归方法的 MATLAB 实现过程。
根据回归方法中因变量的个数和回归函数的类型(线性或非线性)可将回归方法分为:一元线性、一元非线性、多元回归。另外还有两种特殊的回归方式,一种在回归过程中可以调整变量数的回归方法,称为逐步回归,另一种是以指数结构函数作为回归模型的回归方法,称为 Logistic 回归。本讲将逐一介绍这几个回归方法。
1. 一元回归
1.1 一元线性回归
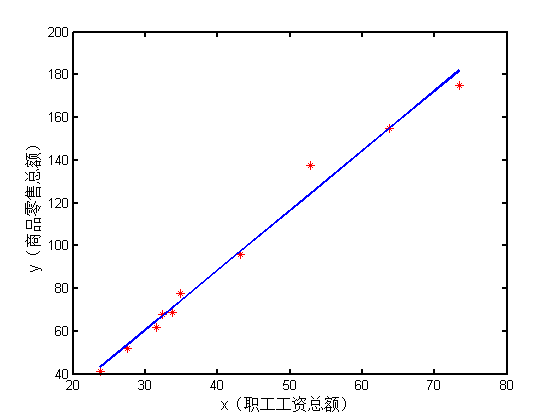
[ 例1 ] 近 10 年来,某市社会商品零售总额与职工工资总额(单位:亿元)的数据见表3-1,请建立社会商品零售总额与职工工资总额数据的回归模型。
表1 商品零售总额与职工工资总额
该问题是典型的一元回归问题,但先要确定是线性还是非线性,然后就可以利用对应的回归方法建立他们之间的回归模型了,具体实现的 MATLAB 代码如下:
(1)输入数据
clc, clear all, close all
x=[23.80,27.60,31.60,32.40,33.70,34.90,43.20,52.80,63.80,73.40];
y=[41.4,51.8,61.70,67.90,68.70,77.50,95.90,137.40,155.0,175.0];
(2)采用最小二乘回归
Figure
plot(x,y,'r*') %作散点图
xlabel('x(职工工资总额)','fontsize', 12) %横坐标名
ylabel('y(商品零售总额)', 'fontsize',12) %纵坐标名
set(gca,'linewidth',2);
% 采用最小二乘拟合
Lxx=sum((x-mean(x)).^2);
Lxy=sum((x-mean(x)).*(y-mean(y)));
b1=Lxy/Lxx;
b0=mean(y)-b1*mean(x);
y1=b1*x+b0;
hold on
plot(x, y1,'linewidth',2);
运行本节程序,会得到如图 1 所示的回归图形。在用最小二乘回归之前,先绘制了数据的散点图,这样就可以从图形上判断这些数据是否近似成线性关系。当发现它们的确近似在一条线上后,再用线性回归的方法进行回归,这样也更符合我们分析数据的一般思路。
图1 职工工资总额和商品零售总额关系趋势图
(3)采用 LinearModel.fit 函数进行线性回归
m2 = LinearModel.fit(x,y)
运行结果如下:
m2 =
Linear regression model:
y ~ 1 + x1
Estimated Coefficients:
Estimate SE tStat pValue
(Intercept) -23.549 5.1028 -4.615 0.0017215
x1 2.7991 0.11456 24.435 8.4014e-09
R-squared: 0.987, Adjusted R-Squared 0.985
F-statistic vs. constant model: 597, p-value = 8.4e-09
(4)采用 regress 函数进行回归
Y=y';
X=[ones(size(x,2),1),x'];
[b, bint, r, rint, s] = regress(Y, X)
运行结果如下:
b =
-23.5493
2.7991
在以上回归程序中,使用了两个回归函数 LinearModel.fit 和 regress。在实际使用中,只要根据自己的需要选用一种就可以了。函数 LinearModel.fit 输出的内容为典型的线性回归的参数。关于 regress,其用法多样,MATLAB 帮助中关于 regress 的用法,有以下几种:
b = regress(y,X)
[b,bint] = regress(y,X)
[b,bint,r] = regress(y,X)
[b,bint,r,rint] = regress(y,X)
[b,bint,r,rint,stats] = regress(y,X)
[...] = regress(y,X,alpha)
输入 y(因变量,列向量),X(1与自变量组成的矩阵)和(alpha,是显著性水平, 缺省时默认0.05)。
输出
bint 是 β0,β1 的置信区间,r 是残差(列向量),rint是残差的置信区间,s包含4个统计量:决定系数 R^2(相关系数为R),F 值,F(1,n-2) 分布大于 F 值的概率 p,剩余方差 s^2 的值。也可由程序 sum(r^2)/(n-2) 计算。其意义和用法如下:R^2 的值越接近 1,变量的线性相关性越强,说明模型有效;如果满足
则认为变量y与x显著地有线性关系,其中 F1-α(1,n-2) 的值可查F分布表,或直接用 MATLAB 命令 finv(1-α,1, n-2) 计算得到;如果 p<α 表示线性模型可用。这三个值可以相互印证。s^2 的值主要用来比较模型是否有改进,其值越小说明模型精度越高。
1.2 一元非线性回归
在一些实际问题中,变量间的关系并不都是线性的,此时就应该用非线性回归。用非线性回归首先要解决的问题是回归方程中的参数如何估计。下面通过一个实例来说明如何利用非线性回归技术解决实例的问题。
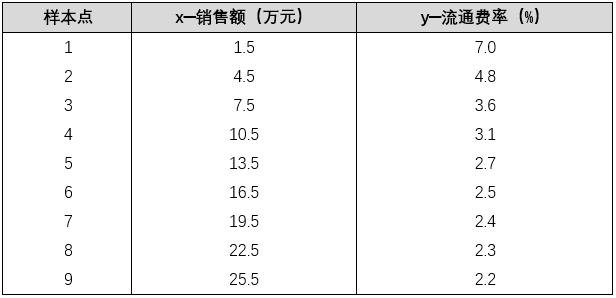
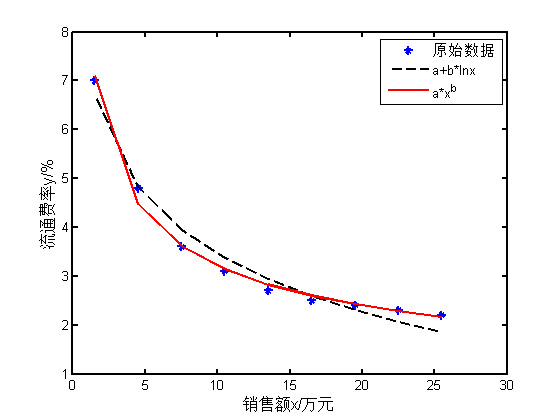
[ 例2 ] 为了解百货商店销售额 x 与流通率(这是反映商业活动的一个质量指标,指每元商品流转额所分摊的流通费用)y 之间的关系,收集了九个商店的有关数据(见表2)。请建立它们关系的数学模型。
表2 销售额与流通费率数据
图2 销售额与流通费率之间的关系图
为了得到 x 与 y 之间的关系,先绘制出它们之间的散点图,如图 2 所示的"雪花"点图。由该图可以判断它们之间的关系近似为对数关系或指数关系,为此可以利用这两种函数形式进行非线性拟合,具体实现步骤及每个步骤的结果如下:
(1)输入数据
clc, clear all, close all
x=[1.5, 4.5, 7.5,10.5,13.5,16.5,19.5,22.5,25.5];
y=[7.0,4.8,3.6,3.1,2.7,2.5,2.4,2.3,2.2];
plot(x,y,'*','linewidth',2);
set(gca,'linewidth',2);
xlabel('销售额x/万元','fontsize', 12)
ylabel('流通费率y/%', 'fontsize',12)
(2)对数形式非线性回归
m1 = @(b,x) b(1) + b(2)*log(x);
nonlinfit1 = fitnlm(x,y,m1,[0.01;0.01])
b=nonlinfit1.Coefficients.Estimate;
Y1=b(1,1)+b(2,1)*log(x);
hold on
plot(x,Y1,'--k','linewidth',2)
运行结果如下:
nonlinfit1 =
Nonlinear regression model:
y ~ b1 + b2*log(x)
Estimated Coefficients:
Estimate SE tStat pValue
b1 7.3979 0.26667 27.742 2.0303e-08
b2 -1.713 0.10724 -15.974 9.1465e-07
R-Squared: 0.973, Adjusted R-Squared 0.969
F-statistic vs. constant model: 255, p-value = 9.15e-07
(3)指数形式非线性回归
m2 = 'y ~ b1*x^b2';
nonlinfit2 = fitnlm(x,y,m2,[1;1])
b1=nonlinfit2.Coefficients.Estimate(1,1);
b2=nonlinfit2.Coefficients.Estimate(2,1);
Y2=b1*x.^b2;
hold on
plot(x,Y2,'r','linewidth',2)
legend('原始数据','a+b*lnx','a*x^b')
运行结果如下:
nonlinfit2 =
Nonlinear regression model:
y ~ b1*x^b2
Estimated Coefficients:
Estimate SE tStat pValue
b1 8.4112 0.19176 43.862 8.3606e-10
b2 -0.41893 0.012382 -33.834 5.1061e-09
R-Squared: 0.993, Adjusted R-Squared 0.992
F-statistic vs. zero model: 3.05e+03, p-value = 5.1e-11
在该案例中,选择两种函数形式进行非线性回归,从回归结果来看,对数形式的决定系数为 0.973 ,而指数形式的为 0.993 ,优于前者,所以可以认为指数形式的函数形式更符合 y 与 x 之间的关系,这样就可以确定他们之间的函数关系形式了。
2. 多元回归
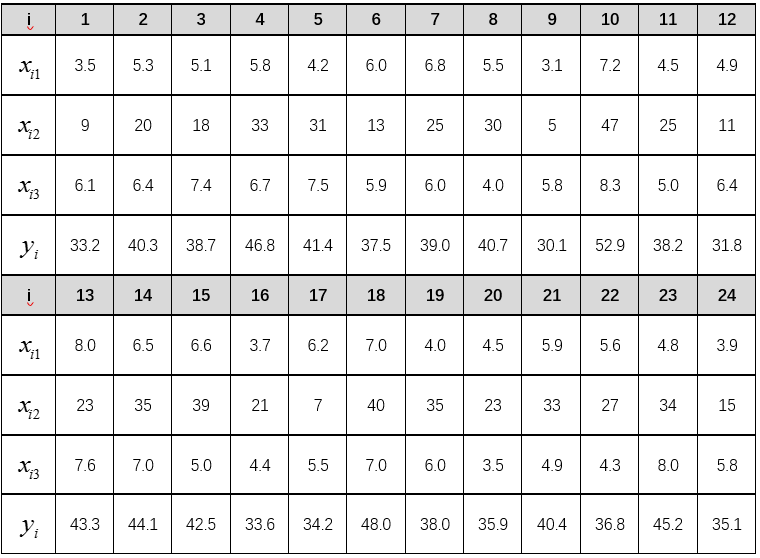
[ 例3 ] 某科学基金会希望估计从事某研究的学者的年薪 Y 与他们的研究成果(论文、著作等)的质量指标 X1、从事研究工作的时间 X2、能成功获得资助的指标 X3 之间的关系,为此按一定的实验设计方法调查了 24 位研究学者,得到如表3 所示的数据( i 为学者序号),试建立 Y 与 X1 , X2 , X3 之间关系的数学模型,并得出有关结论和作统计分析。
表3 从事某种研究的学者的相关指标数据
该问题是典型的多元回归问题,但能否应用多元线性回归,最好先通过数据可视化判断他们之间的变化趋势,如果近似满足线性关系,则可以执行利用多元线性回归方法对该问题进行回归。具体步骤如下:
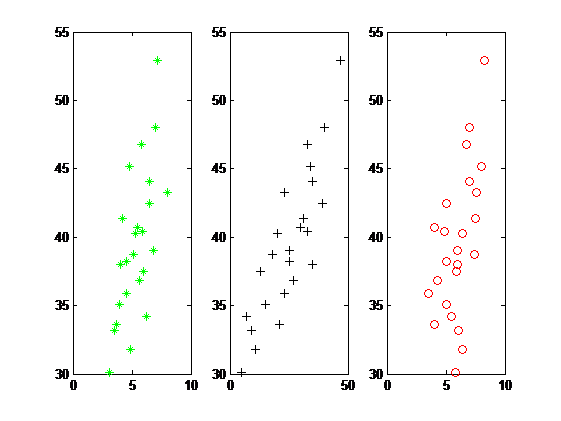
(1)作出因变量 Y 与各自变量的样本散点图
作散点图的目的主要是观察因变量 Y 与各自变量间是否有比较好的线性关系,以便选择恰当的数学模型形式。图3 分别为年薪 Y 与成果质量指标 X1、研究工作时间 X2、获得资助的指标 X3 之间的散点图。从图中可以看出这些点大致分布在一条直线旁边,因此,有比较好的线性关系,可以采用线性回归。绘制图3的代码如下:
subplot(1,3,1),plot(x1,Y,'g*'),
subplot(1,3,2),plot(x2,Y,'k+'),
subplot(1,3,3),plot(x3,Y,'ro'),
图3 因变量Y与各自变量的样本散点图
(2)进行多元线性回归
这里可以直接使用 regress 函数执行多元线性回归,具体代码如下:
x1=[3.5 5.3 5.1 5.8 4.2 6.0 6.8 5.5 3.1 7.2 4.5 4.9 8.0 6.5 6.5 3.7 6.2 7.0 4.0 4.5 5.9 5.6 4.8 3.9];
x2=[9 20 18 33 31 13 25 30 5 47 25 11 23 35 39 21 7 40 35 23 33 27 34 15];
x3=[6.1 6.4 7.4 6.7 7.5 5.9 6.0 4.0 5.8 8.3 5.0 6.4 7.6 7.0 5.0 4.0 5.5 7.0 6.0 3.5 4.9 4.3 8.0 5.0];
Y=[33.2 40.3 38.7 46.8 41.4 37.5 39.0 40.7 30.1 52.9 38.2 31.8 43.3 44.1 42.5 33.6 34.2 48.0 38.0 35.9 40.4 36.8 45.2 35.1];
n=24; m=3;
X=[ones(n,1),x1',x2',x3'];
[b,bint,r,rint,s]=regress(Y',X,0.05);
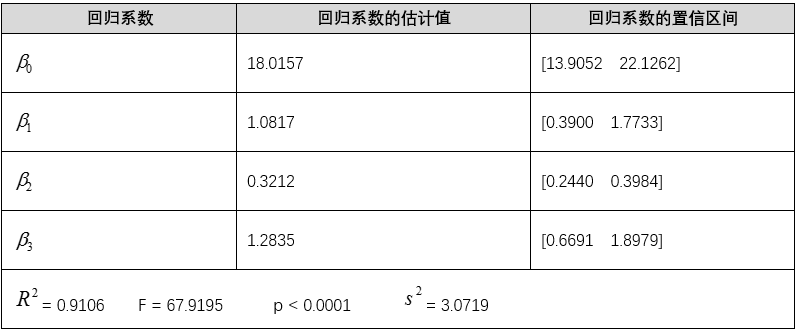
运行后即得到结果如表4所示。
表4 对初步回归模型的计算结果
计算结果包括回归系数 b = (β0,β1,β2,β3) = (18.0157, 1.0817, 0.3212, 1.2835)、回归系数的置信区间,以及统计变量 stats(它包含四个检验统计量:相关系数的平方R^2,假设检验统计量 F,与 F 对应的概率 p,s^2 的值)。因此我们得到初步的回归方程为:
由结果对模型的判断:
回归系数置信区间不包含零点表示模型较好,残差在零点附近也表示模型较好,接着就是利用检验统计量 R,F,p 的值判断该模型是否可用。
1)相关系数 R 的评价:本例 R 的绝对值为 0.9542 ,表明线性相关性较强。
2)F 检验法:当 F > F1-α(m,n-m-1) ,即认为因变量 y 与自变量 x1,x2,...,xm 之间有显著的线性相关关系;否则认为因变量 y 与自变量 x1,x2,...,xm 之间线性相关关系不显著。本例 F=67.919 > F1-0.05( 3,20 ) = 3.10。
3)p 值检验:若 p < α(α 为预定显著水平),则说明因变量 y 与自变量 x1,x2,...,xm之间显著地有线性相关关系。本例输出结果,p<0.0001,显然满足 p<α=0.05。
以上三种统计推断方法推断的结果是一致的,说明因变量 y 与自变量之间显著地有线性相关关系,所得线性回归模型可用。s^2 当然越小越好,这主要在模型改进时作为参考。
3. 逐步归回
[ 例4 ] (Hald,1960)Hald 数据是关于水泥生产的数据。某种水泥在凝固时放出的热量 Y(单位:卡/克)与水泥中 4 种化学成品所占的百分比有关:
在生产中测得 12 组数据,见表5,试建立 Y 关于这些因子的"最优"回归方程。
表5 水泥生产的数据
对于例 4 中的问题,可以使用多元线性回归、多元多项式回归,但也可以考虑使用逐步回归。从逐步回归的原理来看,逐步回归是以上两种回归方法的结合,可以自动使得方程的因子设置最合理。对于该问题,逐步回归的代码如下:
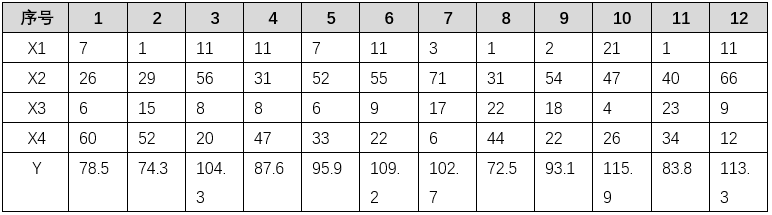
X=[7,26,6,60;1,29,15,52;11,56,8,20;11,31,8,47;7,52,6,33;11,55,9,22;3,71,17,6;1,31,22,44;2,54,18,22;21,47,4,26;1,40,23,34;11,66,9,12]; %自变量数据
Y=[78.5,74.3,104.3,87.6,95.9,109.2,102.7,72.5,93.1,115.9,83.8,113.3]; %因变量数据
Stepwise(X,Y,[1,2,3,4],0.05,0.10)% in=[1,2,3,4]表示X1、X2、X3、X4均保留在模型中
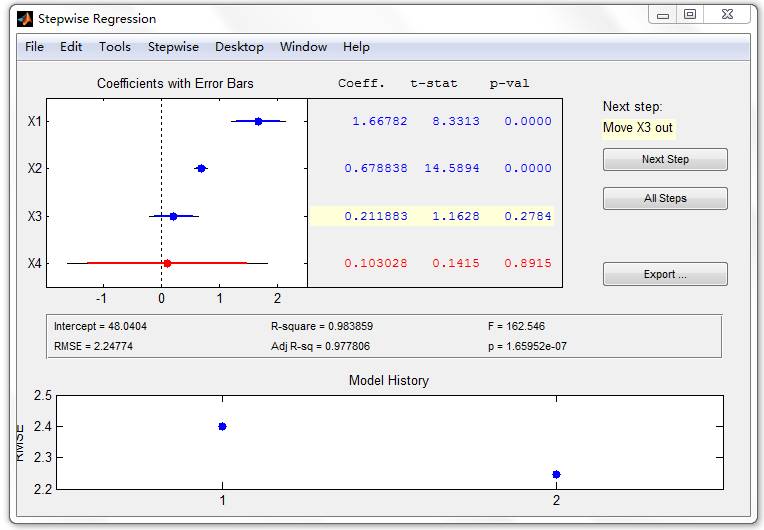
程序执行后得到下列逐步回归的窗口,如图 4 所示。
图4 逐步回归操作界面
在图 4 中,用蓝色行显示变量 X1、X2、X3、X4 均保留在模型中,窗口的右侧按钮上方提示:将变量X3剔除回归方程(Move X3 out),单击 Next Step 按钮,即进行下一步运算,将第 3 列数据对应的变量 X3 剔除回归方程。单击 Next Step 按钮后,剔除的变量 X3 所对应的行用红色表示,同时又得到提示:将变量 X4 剔除回归方程(Move X4 out),单击 Next Step 按钮,这样一直重复操作,直到 "Next Step" 按钮变灰,表明逐步回归结束,此时得到的模型即为逐步回归最终的结果。
4. Logistic 回归
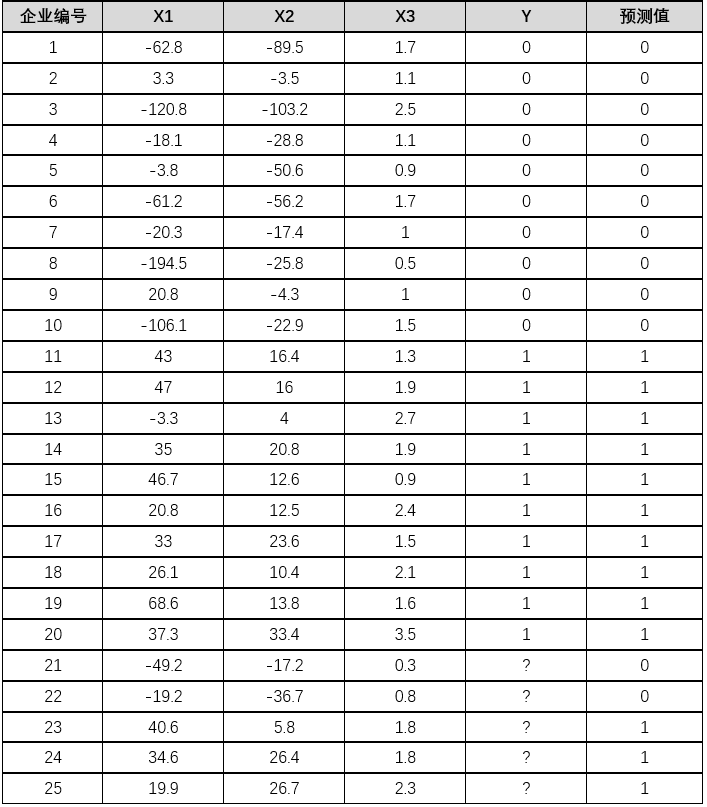
[ 例5 ] 企业到金融商业机构贷款,金融商业机构需要对企业进行评估。评估结果为 0 , 1 两种形式,0 表示企业两年后破产,将拒绝贷款,而 1 表示企业 2 年后具备还款能力,可以贷款。在表 6 中,已知前 20 家企业的三项评价指标值和评估结果,试建立模型对其他 5 家企业(企业 21-25)进行评估。
表6 企业还款能力评价表
对于该问题,很明显可以用 Logistic 模型来回归,具体求解程序如下:
% logistic回归Matlab实现程序
%% 数据准备
clc, clear, close all
X0=xlsread('logistic_ex1.xlsx', 'A2:C21'); % 回归模型的输入
Y0=xlsread('logistic_ex1.xlsx', 'D2:D21'); % 回归模型的输出
X1=xlsread('logistic_ex1.xlsx', 'A2:C26'); % 预测数据输入
%% logistics函数
GM = fitglm(X0,Y0,'Distribution','binomial');
Y1 = predict(GM,X1);
%% 模型的评估
N0 =1:size(Y0,1); N1= 1:size(Y1,1);
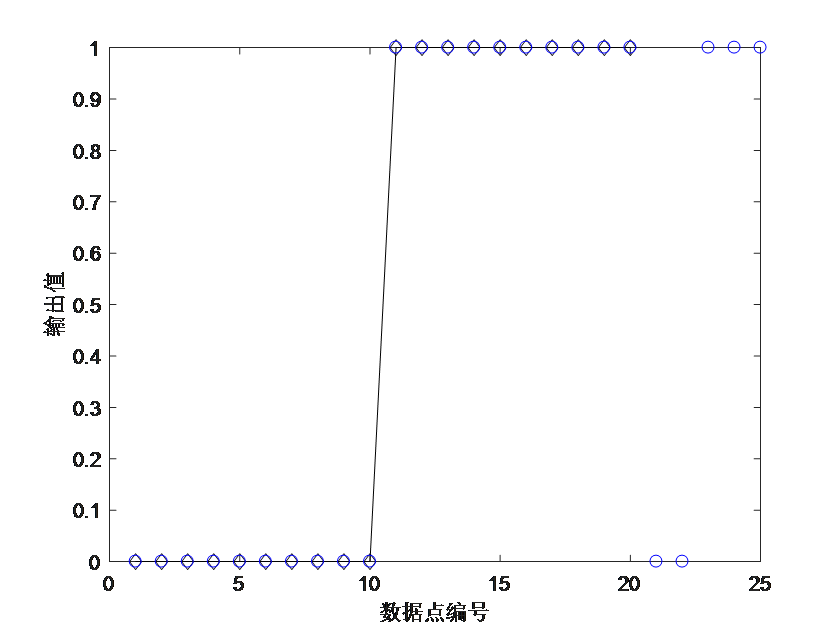
plot(N0', Y0, '-kd');
hold on; scatter(N1', Y1, 'b')
xlabel('数据点编号'); ylabel('输出值');
得到的回归结果与原始数据的比较如图5所示。
图5 回归结果与原始数据的比较图
5. 小结
本讲主要介绍数学建模中常用的几种回归方法。在使用回归方法的时候,首先可以判断自变量的个数,如果超过 2 个,则需要用到多元回归的方法,否则考虑用一元回归。然后判断是线性还是非线性,这对于一元回归是比较容易的,而对于多元,往往是将其他变量保持不变,将多元转化为一元再去判断是线性还是非线性。如果变量很多,而且复杂,则可以首先考虑多元线性回归,检验回归效果,也可以用逐步回归。总之,用回归方法比较灵活,根据具体情景还是比较容易找到合适的方法的。
博客地址:http://blog.yoqi.me/?p=3612


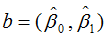
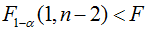
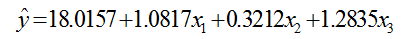
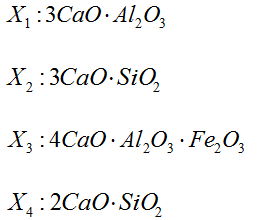
这篇文章还没有评论