生日悖论
之前接触过,一个40个人的班上,总会有人同一天过生日,最后计算到,40人中,至少同一天过生日的概率非常大(超过80%),这也就是生日悖论。
那么今天又遇到同样的问题,被人问到一下子卡住了。
问题:n个人中,至少两个人有相同生日的概率是多少?当概率大于1/2的时候,n取最小多少?
这个概率一下子没想到,所以搜索了一下:
N个人中,有两个人生日相同的概率是没有人生日在同一天的概率是:C(365,n)n!/(365)^n 所以至少有两个人生日在同一天的概率为:1-C(365,n)n!/(365)^n
https://www.zybang.com/question/61511bc59391c0f7ac9c0767094e49de.html
接下来就是编程计算了,下面给出java代码、matlab代码、python代码,R代码,C语言略:
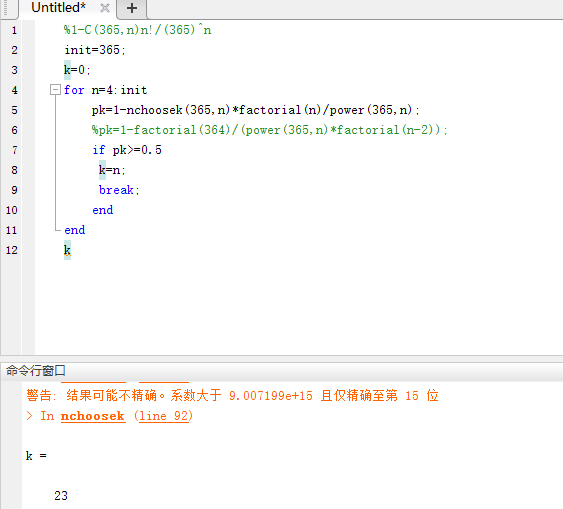
matlab code:
R code:
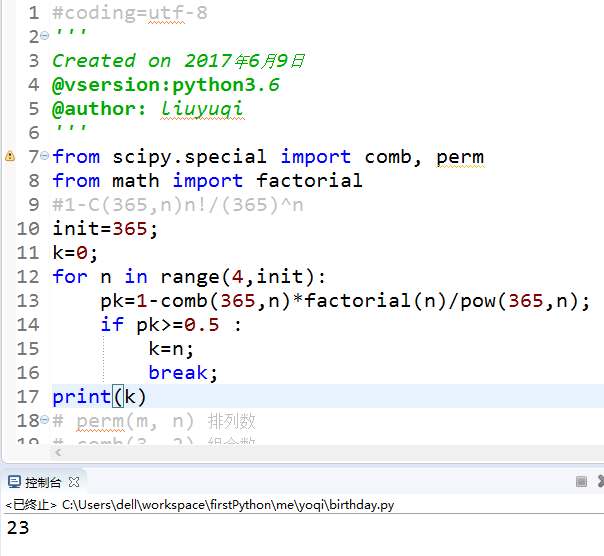
python code:
python注意格式,所以这里截图:
java code:
package me.yoqi;
public class Test {
public static void main(String args[]) {
int init = 365;
double pk = 0;
for (int n = 3; n < init; n++) {
pk = 1 - combination(365,n ) * factorial(n) / Math.pow(365, n);
if (pk >= 0.5) {
System.out.println("最小K:" + n);
break;
}
}
}
int init = 365;
double pk = 0;
for (int n = 3; n < init; n++) {
pk = 1 - combination(365,n ) * factorial(n) / Math.pow(365, n);
if (pk >= 0.5) {
System.out.println("最小K:" + n);
break;
}
}
}
/**
* 计算阶乘数,即n! = n * (n-1) * ... * 2 * 1
*
* @param n
* @return
*/
private static long factorial(int n) {
return (n > 1) ? n * factorial(n - 1) : 1;
}
* 计算阶乘数,即n! = n * (n-1) * ... * 2 * 1
*
* @param n
* @return
*/
private static long factorial(int n) {
return (n > 1) ? n * factorial(n - 1) : 1;
}
/**
* 计算排列数,即A(n, m) = n!/(n-m)!
*
* @param n
* @param m
* @return
*/
public static long arrangement(int n, int m) {
return (n >= m) ? factorial(n) / factorial(n - m) : 0;
}
* 计算排列数,即A(n, m) = n!/(n-m)!
*
* @param n
* @param m
* @return
*/
public static long arrangement(int n, int m) {
return (n >= m) ? factorial(n) / factorial(n - m) : 0;
}
/**
* 计算组合数,即C(n, m) = n!/((n-m)! * m!)
*
* @param n
* @param m
* @return
*/
public static long combination(int n, int m) {
return (n >= m) ? factorial(n) / factorial(n - m) / factorial(m) : 0;
}
}
* 计算组合数,即C(n, m) = n!/((n-m)! * m!)
*
* @param n
* @param m
* @return
*/
public static long combination(int n, int m) {
return (n >= m) ? factorial(n) / factorial(n - m) / factorial(m) : 0;
}
}
注意:
(1)java无法计算365!阶乘,考虑用bigInteger处理比较麻烦。所以说涉及到大数计算,还是考虑专业数学工具,涉及到大数据分析,还是需要分布式计算。
(2)只是为了满足某些看客,编程不在乎何种语言,达到目的即可。
代码仓库:http://git.yoqi.me/lyq/yunyin
博客地址:http://blog.yoqi.me/?p=3184


这篇文章还没有评论